What is flexural strength?
Flexural strength is a material property, Which is defined as “the maximum stress in a material just before it yields in a bending test”. Flexural strength is also known as bending strength or transverse rupture strength.

When a specimen like a beam or a rod, is bent it undergoes or experiences a variety of stresses across its depth. At the inside of the bend, the stress will be at its maximum compressive stress, while at the opposite side the stress will be at its maximum tensile stress value.
These inner and outer edges of the specimen are called extreme fibers. Most materials fail due to tensile stress before they fail under compressive stress. This is caused by small defects of various sizes at the surface, which will grow under tensile stress.
Therefore the maximum tensile stress value under bending before the beam or rod fails is considered its flexural strength.
Flexural strength Test
There are mainly two types of flexural strength tests are present, A long rectangular sample of the material is supported at its ends, so there is no support in the middle, but the ends are sturdy. A load or force is then applied to the middle section until the material breaks. which are explained in detail below.
Flexural strength test types:
- Three-point flexural strength test
- Four-point flexural strength test
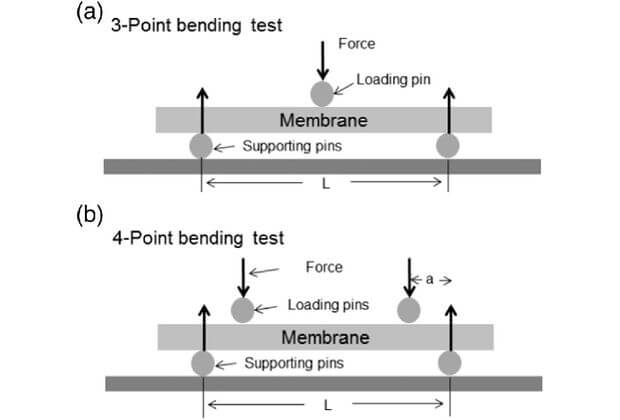
Three-Point flexural Test
In a three-point bending strength test, a continually increasing load is applied at the center of the sample till there is a breakage or permanent bend in the material. A flexural test machine can apply increasing amounts of force and precisely record the amount of force at the point of breaking.
Four-Point Test
A four-point bending test is very similar to a three-point test, But except the load is applied at two points simultaneously, again towards the center of the sample. It’s easiest to calculate the flexural strength when one load or force is applied one-third of the way between the supports and the second is applied two-thirds of the way between them. So in this example, the middle third of the sample would have forces applied at either side of it.
Three-Point Test Flexural Strength Calculation
For a three-point test, the flexural strength (given the symbol σ) can be calculated using:
σ = 3FL / 2wd2
This might look scary at first, but once you know what each symbol means, it’s quite a simple equation to use.
F means the maximum force applied, L is the length of the sample, w is the width of the sample and d is the depth of the sample. So to calculate the flexural strength (σ), multiply the force by the length of the sample, and then multiply this by three. Then multiply the depth of the sample by itself (i.e., square it), multiply the result by the width of the sample and then multiply this by two. Finally, divide the first result by the second.
In SI units, lengths, widths, and depths will be measured in meters, while force will be measured in newtons, with a result in pascals (Pa), or newtons per meter squared. In Imperial units, lengths, widths, and depths will be measured in inches, and force will be measured in pounds-force, with a result in pounds per square inch.
Four-Point Test Flexural Strength Calculation
The four-point test uses the same symbols as the three-point test calculation. But with the assumption that the two loads or forces are applied so they split the sample into thirds, it looks much simpler:
σ = FL / wd2
Note that this is exactly the same as the flexural stress formula for three-point tests, but without the factor of 3/2. So simply multiply the force applied by the length, and then divide this by the width of the material multiplied by the depth of it squared.
Also Read – Pre-stressed concrete -Types of Pre-stressed concrete systems

